Shor 算法

---

RSA 算法是当前使用范围最广的加密算法之一，它是一种非对称加密算法，使用公钥对信息加密，使用私钥对密文解密，它的加密原理以及安全性主要是建立在“在经典计算中很难对两个大素数的乘积进行因式分解”这一问题之上，而 Shor 算法则证明了使用量子算法可以在多项式时间内解决这个问题，从而动摇了 RSA 算法的地位。
Shor 算法将分解质因数问题转化为“找到模函数的周期”问题，而量子计算可以高效的实现“寻找函数周期”这一任务。Shor 算法是一种混合算法，其主体部分是在经典计算机上运行，关键部分使用了量子计算来寻找模函数周期。需要明确的是，目前还没有足够容错的硬件设备可以对真实秘钥进行破解，但 Shor 算法展示了充分的潜力，目前的真机实验还处在分解 $15=3\ast 5$ 的阶段。

Shor 算法的步骤

假设问题是因数分解某个数 N，并且我们知道如何找到任何模函数的周期，那么对 N 进行因数分解的问题可以规约为寻找 N 的任意因子的这么一个简单问题。这个问题可以利用模函数的周期来求解。步骤如下：

1. 选择一个随机数 $a<N$;
2. 使用扩展欧几里得算法计算 $gcd(a,N)$;
3. 如果 $gcd(a,N)\ne 1$，即 a 与 N 不互素，则找到了 N 的因子，算法结束；
4. 否则寻找模函数 $f(n):=a^n(modN)$ 的周期 r；
5. 如果 r 是奇数，或者 $a^{\frac{r}{2}}=-1(modN)$，本轮算法失败，选择一个新的随机数重新开始；
6. 否则，经典数论保证了 $gcd(a^{\frac{r}{2}+1},N)$ 和 $gcd(a^{\frac{r}{2}-1},N)$ 都是 N 的非平凡因子。

以分解 21 为例：

1. 选择 a=2；
2. $gcd(a,N)=1$;
3. 忽略；
4. 计算模函数 $f(n):=a^n(modN)$ 的周期 r 为 6；
5. 不满足 5 的条件，继续；
6. $gcd(a^{\frac{r}{2}+1},N)=gcd(9,21)=3$ 和 $gcd(a^{\frac{r}{2}-1},N)=gcd(7,21)=7$，3 和 7 是 21 的两个非平凡的因子。

可以看出寻找任意模函数的周期是 Shor 算法的关键，要高效的完成这一步骤需要使用量子算法，而其他步骤可以使用经典算法高效的计算完成。

求阶问题

本小节介绍如何使用量子算法实现寻找模函数 $f(n):=a^n(modN)$ 的周期 r，该问题被成为求阶问题，r即所求的阶。

问题输入： 正整数 N 和 a，且满足 $a<N$, $gcd(N,a)=1$
问题输出： 最小的正整数 r 使得：$a^r=1(modN)$

转化为相位估计

求阶量子算法就是将相位估计应用到如下的酉算子上：

$$U|y⟩=|xy(modN)⟩$$

其中 $y\in {0,1}^L$，L 是表示 N 所需的比特数。可以计算得出

$$|u_s⟩=\frac{1}{\sqrt{r}}\sum _{k=0}^{r-1}exp[\frac{-2\pi isk}{r}]|x^{k}modN⟩$$

是 U 的特征向量。且：

$$\begin{gathered} U|u_s⟩=\frac{1}{\sqrt{r}}\sum _{k=0}^{r-1}exp[\frac{-2\pi isk}{r}]|x^{k+1}modN⟩ \\ =exp[\frac{2\pi is}{r}]|u_s⟩ \end{gathered}$$

特征值是 $exp[\frac{2\pi is}{r}]$。利用相位估计算法我们可以得出 $\frac{s}{r}$，然后使用连分式算法即可得到 r 的值，但是此时我们要使用相位估计需要先知道 r 才能制备特征向量。注意到：

$$\frac{1}{\sqrt{r}}\sum _{s=0}^{r-1}|u_s⟩=|1⟩$$

左式是特征向量的叠加态，当特征向量以叠加态执行相位估计时，得出的结果也是特征值的叠加态，此时观察到的任一结果均可以用来求出 r。上式表明我们可以在相位估计的电路中，简单的把特征向量置为 $|1⟩$。

电路实现

根据前一小节的内容可以看到，求阶算法本身是相位估计的应用，因此电路实现上与相位估计相同。

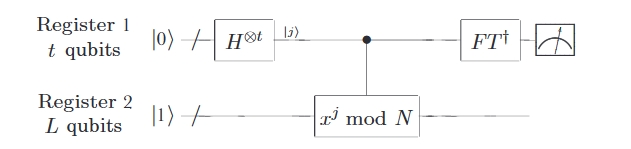
现假设我们正在求解 15 的因式分解，我们按 shor 算法的步骤随机选取了 a=8，则代码实现为：

import std;
import qft;

int a = 8;
int N = 15;
int precision = 4;

procedure c_a8mod15(qbit c, qbit q0, qbit q1, qbit q2, qbit q3) {
    ctrl SWAP(c, q0, q1);
    ctrl SWAP(c, q1, q2);
    ctrl SWAP(c, q2, q3);
} deriving gate 

procedure prepare_eigenvector(qbit ev[]){
    X(ev[0]);
}

procedure phase_estimation(){
    qbit ev[4];
    qbit reg[precision];
    prepare_eigenvector(ev);

    for i in 0:precision {
        H(reg[i]);
        int repeat = 2 ** i;
        for j in 0:repeat {
            c_a8mod15(reg[i], ev[0], ev[1], ev[2], ev[3]);
        }
    }
    qft_inv(reg);
    for i in precision-1:-1:-1 {
        M(reg[i]);
    }
}

procedure main() {
    phase_estimation();
}

对应的 python 代码为：

from fractions import Fraction
from math import gcd

from isqtools import IsqCircuit
from isqtools.backend import NumpyBackend

a = 8
N = 15


FACTOR_FOUND = False
ATTEMPT = 0
while not FACTOR_FOUND:
    ATTEMPT += 1
    print(f"\nAttempt {ATTEMPT}")

    qc = IsqCircuit(
        file="shor_8mod15.isq", backend=NumpyBackend(), sample=True, shots=1
    )
    result = qc.measure()
    measured = result.popitem()[0]
    phase = int(measured, 2) / 2**4
    frac = Fraction(phase).limit_denominator(N)
    r = frac.denominator
    if phase != 0:
        guess = gcd(a ** (r // 2) - 1, N)
        print(f"Guess {guess}")
        if guess not in [1, N] and (N % guess) == 0:
            # Guess is a factor!
            factor = N / guess
            print(f"Found factor: {guess} * {int(factor)} = {N}")
            FACTOR_FOUND = True
        else:
            print("guess failed, try again.")

Attempt 1
Guess 1
guess failed, try again.

Attempt 2

Attempt 3
Guess 3
Found factor: 3 * 5 = 15

---