Deutsch 算法

问题介绍

Deutsch 问题表述为：给定一个单比特输入、单比特输出的布尔函数，通过尽可能少的查询次数来确定该函数是平衡函数还是常函数。
这种单比特输入、单比特输出的布尔函数有 4 种：

x	$f_0$	$f_1$	$f_x$	$f_{\bar{x}}$
0	0	1	0	1
1	0	1	1	0

其中，$f_0$ 和 $f_1$ 是 常函数，也即它们总是输出一个常数；而 $f_x$ 和 $f_{\bar{x}}$ 是 平衡函数，就是说输入为 0 和 1 时，它的输出真值表中 0 和 1 的个数相同。
如果使用经典计算机来解决 Deutsch 问题，那么至少需要查询两次才能确定函数的类型：首先查看输入为 0 时函数的输出，然后查看输入为 1 时的输出。但是在量子计算中，这个问题只需要使用一次查询即可知道结果。原始的 Deutsch 只处理单比特布尔的情形，而 Deutsch-Jozsa（DJ）算法泛化了处理 n 比特输入的布尔函数的方法，DJ 算法通过一次查询就可以解决这个问题。

算法实现

Deutsch 算法的电路实现如下所示：

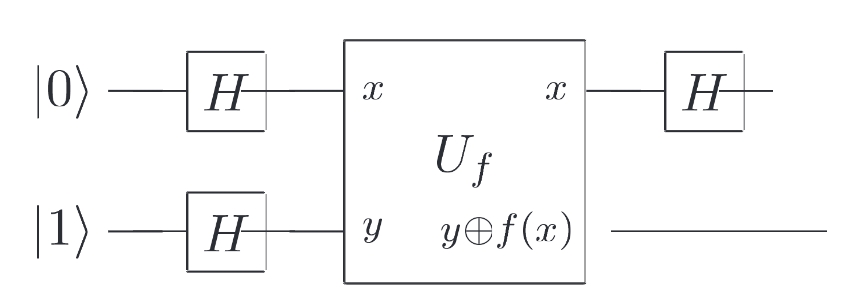
我们定义了一个酉算子 $U_f$ 来表示我们需要查询的函数，可知单比特输入单比特输出的函数是不可逆的，因此酉算子 $U_f$ 需要第二个量子比特，并且该算子执行操作 $U_f|x⟩|y⟩=|x⟩|f(x)\oplus y⟩$ 下面逐步分析此电路，系统被初始化为状态

$$|{\psi }_0⟩=|10⟩$$

在第一步应用两个 Hadamard 门后，系统状态为：

$$\begin{gathered} |{\psi }_1⟩=|-⟩|+⟩=\frac{1}{2}(|0⟩-|1⟩)(|0⟩+|1⟩) \\ =\frac{1}{2}(|0⟩-|1⟩)|0⟩+\frac{1}{2}(|0⟩-|1⟩)|1⟩ \end{gathered}$$

然后应用了 $U_f$ 门

$$|{\psi }_2⟩=\frac{1}{2}(|0\oplus f(0)⟩-|1\oplus f(0)⟩)|0⟩+\frac{1}{2}(|0\oplus f(1)⟩-|1\oplus f(1)⟩)|1⟩$$

注意到对于单比特 $a\in \{0,1\}$，有 $|0\oplus a⟩-|1\oplus a⟩=(-1{)}^a(|0⟩-|1⟩)$，该关系同样适用于单比特输出的 f(x) 函数，因此有：

$$\begin{gathered} |{\psi }_2⟩=\frac{1}{2}(-1{)}^{f(0)}(|0⟩-|1⟩)|0⟩+\frac{1}{2}(-1{)}^{f(1)}(|0⟩-|1⟩)|1⟩ \\ =|-⟩\left(\frac{(-1{)}^{f(0)}|0⟩+(-1{)}^{f(1)}|1⟩}{\sqrt{2}}\right) \end{gathered}$$

这里发生了相位反冲现象，$U_f$ 原本应该对左下角的比特做操作，这里我们计算得出左上角的比特会发生一定的变化。更进一步的简化公式：

$$\begin{gathered} |{\psi }_2⟩=(-1{)}^{f(0)}|-⟩\left(\frac{|0⟩+(-1{)}^{f(0)\oplus f(1)}|1⟩}{\sqrt{2}}\right) \\ =\{\begin{array}{ll}(-1{)}^{f(0)}|-⟩|+⟩& \text{if }f(0)\oplus f(1)=0\\ (-1{)}^{f(0)}|-⟩|-⟩& \text{if }f(0)\oplus f(1)=1\end{array} \end{gathered}$$

应用最后一个 Hadamard 门到第一个量子比特，我们得到状态：

$$|{\psi }_3⟩=\{\begin{array}{ll}(-1{)}^{f(0)}|-⟩|0⟩& \text{if }f(0)\oplus f(1)=0\\ (-1{)}^{f(0)}|-⟩|1⟩& \text{if }f(0)\oplus f(1)=1\end{array}$$

我们注意到对于常函数来说 $f(0)\oplus f(1)=0$，而平衡函数 $f(0)\oplus f(1)=1$，因此根据上式，当第一个比特被测量时，若测量结果是 0，则函数是常函数，若测量结果是 1，函数是平衡函数。

示例代码

在这里我们假设想要查询的函数是 $f_{\bar{x}}$，即 $f(0)=1,f(1)=0$，那么有代码如下：

import std;

oracle u(1, 1) = [1, 0];

procedure main(){
    qbit q[2];
    X(q[1]);
    H(q);
    u(q[0], q[1]);
    H(q[0]);
    M(q[0]);    
}

---