量子计算基础知识

量子算子

在量子计算中，我们可以使用向量来表示量子比特，例如：

$$|0⟩=(\genfrac{}{}{0ex}{}{1}{0}),|1⟩=(\genfrac{}{}{0ex}{}{0}{1})$$

而在基于门的量子计算机中，用来改变量子比特状态的算子是酉矩阵，这些算子也称为“门”。

量子电路

量子电路可以用电路图来表示，量子电路图从左到右绘制和阅读，电路线用一根线来表示，初识状态用 Dirac 符号表示并放在线的左侧。

可以用一个标记了 n 的斜杠穿过电路线，表示 n 个在此状态下的量子比特。对于量子算子来说，一个单量子比特算子用一个跨行的框来表示，框内是表示该算子的字母；二元算子用一个跨越两根量子线的算子框来表示，以此类推。

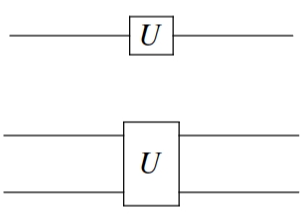
一元算子

现在介绍一些典型的一元算子。

Pauli 算子 X、Y、Z

$$X:=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),Y:=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),Z:=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

可以看到

$$X|0⟩=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)(\genfrac{}{}{0ex}{}{1}{0})=(\genfrac{}{}{0ex}{}{0}{1})=|1⟩$$

因此 X 算子又叫 NOT 算子。

相位偏移算子 R、S、T

注意到对于 Z 算子， $Z|0⟩=|0⟩$, $Z|1⟩=-|1⟩$，因此可以把 Z 算子看做 “把状态向量沿 z 轴旋转 π 弧度”。考虑更加一般的相位偏移算子，当此算子作用于 $|0⟩$ 时，结果保持不变；作用于 $|1⟩$ 时旋转一个角度 $\theta$。此算子可以用矩阵表示为：

$$Phase(\theta ):=\left(\begin{array}{cc}1& 0\\ 0& e^{i\theta }\end{array}\right)$$

特殊的：

• 当 $\theta =\frac{\pi }{4}$ 时为 T 算子。
• 当 $\theta =\frac{\pi }{2}$ 时为 S 算子。
• 当 $\theta =\frac{\pi }{1}$ 时为 Z 算子。

Hadamard 算子

Hadamard 算子，也称 H 算子，在量子计算中至关重要，其矩阵表示为：

$$H:=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$$

可以计算得出

$$H|0⟩=\frac{|0⟩+|1⟩}{\sqrt{2}},H|1⟩=\frac{|0⟩-|1⟩}{\sqrt{2}}$$

H 算子可以将量子比特从确定的计算基状态转换为两个概率均等的状态的叠加态。事实上，H 算子是单量子比特情况下的量子傅里叶变换。

二元算子

现在介绍一些典型的二元算子。

CNOT

控制非（CNOT）算子是一个常用的二元算子，其第一个量子比特称为控制量子比特（control qubit），第二个量子比特称为目标量子比特（target qubit）。如果控制比特处于状态 $|0⟩$，那么什么也不会发生；如果控制比特处于状态 $|1⟩$， 那么它对目标比特执行 NOT 算子。

$$CNOT:=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right)$$

其电路上表示为：

我们尝试着计算如下电路：

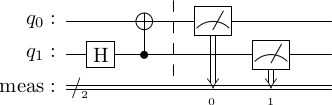
可以得出结果

$$|\psi ⟩=\frac{|00⟩+|11⟩}{\sqrt{2}}$$

测量该电路的两个量子比特，测量结果要么全部是 0 要么全部是 1，事实上我们只需要测量一个比特就知道另一个比特处于什么状态，故而此时这两个量子比特处于纠缠态。可以看出 CNOT 常用来制备纠缠态量子对。

SWAP

SWAP 算子可以交换两个量子比特的状态，例如将 $|01⟩$ 转为 $|10⟩$，其矩阵表示为：

$$SWAP:=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right)$$

其电路图表示为:

另外 SWAP 算子与 CNOT 算子存在关系：

$$SWA{P}_{ij}=CNO{T}_{ij}CNO{T}_{ji}CNO{T}_{ij}$$

三元算子与通用性

现在我们考虑三元算子。

Toffoli 算子

Toffoli 算子又称 CCNOT，和 CNOT 很类似，Toffoli 算子有两个控制位。当两个控制比特均为 1 时，翻转目标比特。
其矩阵表示为：

$$CCNOT:=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right)$$

其电路表示为：

通用性

如同经典计算存在通用的逻辑门与非门，可以组合出其他算子一样。量子计算门往往也是由基础的算子构成的，目前不同量子计算机支持的算子不同，具体可用的门可以参考附录。
另外，基于量子力学原理，量子计算中不存在复制门，因此经典计算中的“扇出”操作无法在量子计算中实现。

---