量子傅里叶变换

定义

量子傅里叶变换（Quantum Fourier Transform, QFT）是量子因子分解和众多其他量子算法的关键部分，可以简单的认为它是离散傅里叶变换（Discrete Fourier Transform, DFT）在量子领域的形式。
令 $N=2^n$，量子傅里叶变换作用在一个量子态 $|X⟩=\sum _{j=0}^{N-1}{x}_j|j⟩$ 上并且把它映射到 $|Y⟩=\sum _{k=0}^{N-1}{y}_k|k⟩$

$$y_k=\frac{1}{\sqrt{N}}\sum _{j=0}^{N-1}{x}_j{e}^{2\pi i\frac{jk}{N}}$$

傅里叶变换的矩阵表示为：

$$\text{QFT}=\frac{1}{\sqrt{N}}\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& \omega & {\omega }^2& \cdots & {\omega }^{N-1}\\ 1& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2(N-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{N-1}& {\omega }^{2(N-1)}& \cdots & {\omega }^{(N-1)(N-1)},\end{array}\right]$$

其中， $\omega =e^{2\pi i/N}$.

从基态的视角来看，QFT 是将计算基映射为频率基的一种操作。从定义上不明显，但是 QFT 也是一个酉变换，因此可以使用量子电路来实现。

电路与实现

由 QFT 的定义可以得知，QFT 将状态 $|j⟩$ 映射到 $\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{e}^{2\pi i\frac{jk}{N}}|k⟩$，举个例子： $QFT|0⟩=\frac{1}{\sqrt{2}}(|0⟩+|1⟩)$，且 $QFT|1⟩=\frac{1}{\sqrt{2}}(|0⟩-|1⟩)$，所以可知，Hadamard 门是在单量子比特时的 QFT。
我们可以用二进制表示法来表示 j，则有 $j=j_1{j}_2{j}_3\cdots j_n$，另外使用二进制表示小数时，有 $0.j_l{j}_{l+1}\cdots j_m=j_l/2+j_{l+1}/4+\cdots +j_m/2^{m-l+1}$，那么对于 QFT 的变换，有

$$\begin{array}{rl}QF{T}_N|j⟩& =\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{e}^{2\pi i\frac{jk}{N}}|k⟩\\ & =\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{e}^{2\pi ij\left(\sum _{l=1}^n{k}_l{2}^{-l}\right)}|k_1\dots k_n⟩\text{用二进制表示法重写}k=k_1\dots k_n,k/2^n=\sum _{l=1}^n{k}_l{2}^{-l}\\ & =\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}\prod _{l=1}^n{e}^{2\pi ij{k}_l{2}^{-l}}|k_1\dots k_l⟩\text{将总和的指数转化为指数的乘积}\\ & =\frac{1}{\sqrt{N}}\underset{l=1}{\overset{n}{⨂}}(|0⟩+e^{2\pi ij{2}^{-l}}|1⟩)\text{重新排列求和与乘积，并且做了展开}\sum _{k=0}^{N-1}=\sum _{k_1=0}^1\sum _{k_2=0}^1\dots \sum _{k_n=0}^1\\ & =\frac{1}{\sqrt{N}}(|0⟩+e^{2\pi i0.j_n}|1⟩)\otimes (|0⟩+e^{2\pi i0.j_{n-1}{j}_n}|1⟩)\otimes \dots \otimes (|0⟩+e^{2\pi i0.j_1\cdots j_n}|1⟩)\end{array}$$

该表示可以转化为量子电路如下:

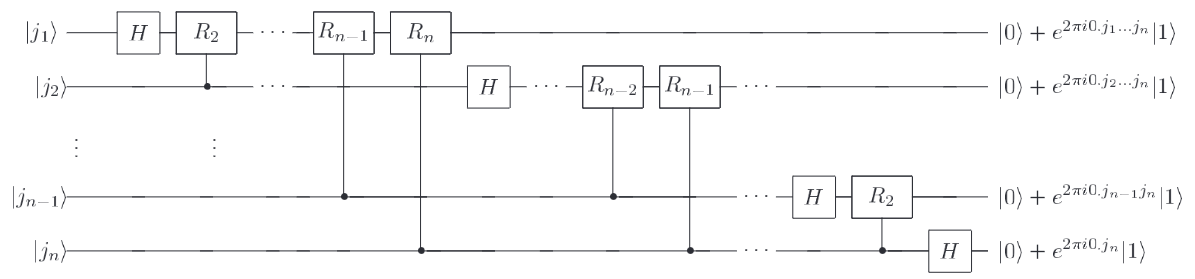
用 IsQ 的代码实现如下：

import std;

procedure R(int k, qbit q) {
    double phase = pi / 2 ** (k - 1);
    ctrl GPhase(phase, q);
} deriving gate

procedure qft(qbit q[]) {
    int len = q.length;
    for i in len-1:-1:-1 {
        H(q[i]);
        for j in 0:i {
            ctrl R(i-j+1, q[j], q[i]);
        }
    }
    for i in 0:len/2 {
        SWAP(q[i], q[len-i-1]);
    }
}

procedure qft_inv(qbit q[]) {
    int len = q.length;
    for i in 0:len/2 {
        SWAP(q[i], q[len-i-1]);
    }
    for i in 0:len {
        for j in 0:i {
            ctrl inv R(i-j+1, q[j], q[i]);
        }
        H(q[i]);
    }
}

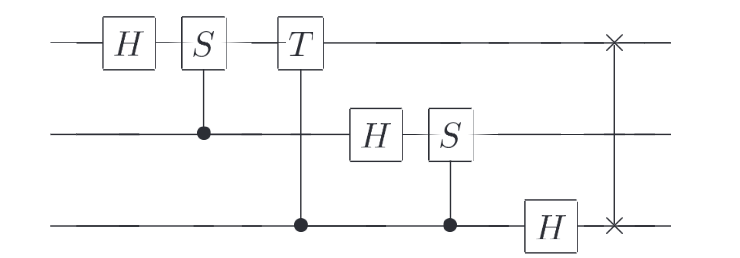
举一个简单的例子，当 n=3 时，QFT 的量子电路如下：

---